
Problem Solving Strategies
-
Look for a pattern
Example:
Solution:Find the sum of the first 100 even positive numbers. The sum of the first 1 even positive numbers is 2 or 1(1+1) = 1(2).
The sum of the first 2 even positive numbers is 2 + 4 = 6 or 2(2+1) = 2(3).
The sum of the first 3 even positive numbers is 2 + 4 + 6 = 12 or 3(3+1) = 3(4).
The sum of the first 4 even positive numbers is 2 + 4 + 6 + 8 = 20 or 4(4+1) = 4(5).Look for a pattern:
The sum of the first 100 even positive numbers is 2 + 4 + 6 + ... = ? or 100(100+1) = 100(101) or 10,100.
- Make an organized list
Example:Find the median of the following test scores: 73, 65, 82, 78, and 93.Solution:Make a list from smallest to largest:
65
73
78 Since 78 is the middle number, the median is 78.
82
93
-
Guess and check
Example:Which of the numbers 4, 5, or 6 is a solution to (n + 3)(n - 2) = 36? Solution:Substitute each number for “n” in the equation. Six is the solution since (6 + 3)(6 - 2) = 36.
-
Make a tableExample:
How many diagonals does a 13-gon have? Solution:Make a table:
Look for a pattern. Hint: If n is the number of sides, thenNumber of sidesNumber of diagonals30425569714820
n(n-3)/2 is the number of diagonals. Explain in words why this works. A 13-gon would have 13(13-3)/2 = 65 diagonals.
- Work
backwards
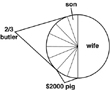
Example:Fortune Problem: a man died and left the following instructions for his fortune, half to his wife; 1/7 of what was left went to his son; 2/3 of what was left went to his butler; the man’s pet pig got the remaining $2000. How much money did the man leave behind altogether? Solution:The pig received $2000.
1/3 of ? = $2000
? = $6000
6/7 of ? = $6000
? = $7000
1/2 of ? = $7000
? = $14,000
-
Use logical reasoning
Example:At the Keep in Shape Club, 35 people swim, 24 play tennis, and 27 jog. Of these people, 12 swim and play tennis, 19 play tennis and jog, and 13 jog and swim. Nine people do all three activities. How many members are there altogether? Solution:Hint: Draw a Venn Diagram with 3 intersecting circles.
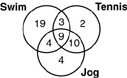
- Draw a diagram
Example:Fortune Problem: a man died and left the following instructions for his fortune, half to his wife; 1/7 of what was left went to his son; 2/3 of what was left went to his butler; the man’s pet pig got the remaining $2000. How much money did the man leave behind altogether?
- Solve a simpler problem
Example:In a delicatessen, it costs $2.49 for a half pound of sliced roast beef. The person behind the counter slices 0.53 pound. What should it cost? Solution:Try a simpler problem. How much would you pay if a half pound of sliced roast beef costs $2 and the person slices 3 pounds? If a half pound costs $2, then one pound would cost 2 x $2 or $4. Multiply by the number of pounds needed to get the total: 3 x $4 = 12.
Now try the original problem: If a half pound costs $2.49, then one pound would cost 2 x $2.49 or $4.98. Multiply by the number of pounds needed to get the total: .53 x $4.98 = $2.6394 or $2.64.
- Read the problem carefully
Know the meaning of all words and symbols in the problem.
Example:List the ten smallest positive composite numbers. Solution:Since positive means greater than 0 and a composite number is a number with more than two whole number factors, the solution is 4, 6, 8, 9, 10, 12, 14, 15, 16, 18. For example, 4 has three factors, 1, 2, and 4.
Sort out information that is not needed.
Example:Last year the Williams family joined a reading club. Mrs. Williams read 20 books. Their son Jed read 12 books. Their daughter Josie read 14 books and their daughter Julie read 7 books. How many books did the children of Mr. and Mrs. Williams read altogether? Solution:You do not need to know how many books Mrs. Williams has read since the question is focusing on the children.
Determine if there is enough information to solve the problem.
Example:How many children do the Williams have? Solution:There is not enough information to solve the problem. You do not know if Josie, Julie, and Jed are the only children.
- Create problem solving
journals
Students record written responses to open-ended items such as those tested on FCAT in mathematics. Student identifies problem solving strategies.

Copyright Statement for this Assessment and Evaluation Services Publication
Authorization for reproduction of this document is hereby granted to persons acting in an official capacity within the State System of Public Education as defined in Section 228.041(1), Florida Statutes. The copyright notice at the bottom of this page must be included in all copies.
The Administrator
Assessment and Evaluation Services
Florida Department of Education
Turlington Building, Room 414
325 West Gaines Street
Tallahassee, Florida 32399-0400
Copyright © 2000
State of Florida
Department of State