Error Pattern Analysis

[ back to Mathematics Dynamic Assement ]

What is it?

Error Pattern Analysis is an assessment approach that allows you to determine whether students are making consistent mistakes when performing basic computations. By pinpointing the pattern of and individual student's errors, you can then directly teach the correct procedure for solving the problem. While there are common errors that students with learning problems make, students may demonstrate error patterns that are individual specific.

Why is it important for students who have learning problems?

Error Pattern Analysis provides you an effective and efficient method for pinpointing specific problems students are having with computation. By determining that your student is consistently using an inaccurate procedure for solving computation problems, you can then provide specific instruction and monitoring to assist the student to use an effective procedure for solving specific types of computations. Additionally, you may discover through error pattern analysis that a student does not have an accurate working knowledge of a major mathematical concept. In other words, specific types of error patterns can cue you that a student not only uses an ineffective procedure to compute a problem, but that the student also does not accurately understand an important math concept. More oftentimes than not, error pattern analysis is much more than a diagnostic tool for determining a student's procedural effectiveness; often, it provides you a window for determining that a student lacks basic conceptual understanding. Students who have difficulty learning mathematics, typically lack important conceptual knowledge. This situation is due to various student learning characteristics as well as instructional factors including: a student's slow rate of processing information relative to instructional pace, lack of sufficient opportunities to respond (practice), lack of specific feedback regarding misunderstanding or non-understanding, anxiety about mathematics, and visual as well as auditory processing difficulties.

How do I do it?

The following steps describe the process for completing error pattern analysis, (Howell, Fox, & Morehead, 1993):

1. Collect a sufficient number of student computation samples for each type of problem you are interested in (at least 3 to 5 samples for each type of problem).

2. As the student works the problems, encourage him/her to talk aloud about what they are doing. Do not cue the student in any way.

3. Record all student responses, both written and verbal.

4. Review the responses and look for patterns among common problem types.

5. Also look for examples of "exceptions" to an apparent pattern (accurate "exceptions" may indicate that the student has partial understanding of the procedure or of a basic concept).

6. List in simple words the patterns you discover, then write beside each pattern why you think it is causing the student problems (e.g. if a student fails to regroup double digit addition problems, it may indicate that he does not understand the concept of place value).

7. Interview the student by asking her to explain how she solved the problem. Hearing what a student was thinking can help you confirm suspected error patterns and how they are impacting your student's success.

What do I look for?

Common types of error patterns for the basic operations include number fact errors, "slips," & "bugs" (Ginsburg, 1987). Number fact errors occur because a student has not mastered the basic facts. "Slips" refer to mistakes made due to lapse in memory or due to impulsivity. These errors usually do not indicate misunderstanding. They usually occur because of particular learning characteristics possessed by a student (e.g. memory deficits, impulsivity, visual/motor integration problems). "Bugs" are most serious because they indicate a student is systematically using an inaccurate/inefficient procedure or strategy. Typically, this type of error pattern indicates non-understanding of an important math concept.

Common Error Patterns (Mercer & Mercer, 1998)

The sums of the ones and tens are each recorded without regrouping. This error pattern reflects a lack of regard for or non-understanding of place value.

All digits are added together. This error pattern reflects an inaccurate procedure (algorithm) and a lack of regard for place value.

Digits are added from left to right. When the sum of a column is greater than 10, the "unit," or "one's" place-holder is carried to the column on the right. This error pattern reflects an inaccurate procedure (algorithm) and a lack of regard for place value.

The smaller number is always subtracted from the larger number without regard to placement of the number (whether it is the upper number, the minuend, or lower number, the subtrahend, is irrelevant). This error pattern reflects an inaccurate procedure (algorithm). Additionally, the student may be using this procedure to avoid regrouping. This may indicate either misunderstanding of the importance of place value or a visual/motor deficit that makes the regrouping process difficult.

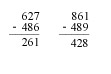
Regrouping is used when it is not needed.

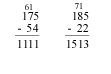
When regrouping is needed more than once, the correct value is not subtracted from the column borrowed from in the second regrouping (e.g. when the upper number in the tens an hundreds column are "borrowed from," the values of those upper numbers are not changed.)

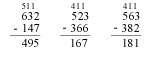
The regrouped number is added to the multiplicand in the tens column prior to performing the multiplication operation.

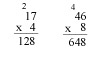
The zero in the quotient is omitted:

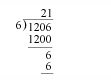
[ back to Mathematics Dynamic Assement ]