Flexible Interview

[ back to Mathematics Dynamic Assessment ]

What is it?/How do I do it?

A flexible interview occurs when the teacher asks the student how he/she solved a particular math problem or set of problems in a non-threatening way. While the flexible interview should be a "comfortable" experience, this does not mean the interview should be without structure and purpose (Bryant, 1996). Several approaches can be selected. The teacher can give a student a problem and ask them to "think aloud" as they solve it. As the student "thinks aloud," the teacher notes errors and potential misconceptions. Based on this data, the teacher then re-teaches the concept/skill. It is important for the teacher to refrain from interrupting the student during the explanation (Kennedy & Tipps, 1994). Interruptions can distract the student's thought process, thereby confounding the information gathered. Additionally, the teacher must refrain from cueing students with subtle verbal and nonverbal behaviors. Some students with learning problems are very adept at responding based on these "cues," potentially leading to an incomplete or misleading picture of the student's problem solving abilities. Although this interview approach can be helpful, verbal expression deficits of many students with learning problems can make "think alouds" very difficult (Bryant, 1996).

A second interview approach, "engaged dialogue," provides these students structure for expressing their thoughts (Zigmond, Vllcorsa, & Silverman, 1981). This semi-structured dialogue between the teacher and the student involves teacher questions that prompt student thinking. Because the purpose of the flexible interview is to understand student thinking, it is important to avoid questions that tempt students to refuse to respond (Liedtke, 1988). For example, questions taking the form of, "Can you….?," or, "Could you…?," provide students to say "no." Because students with math learning problems are typically passive learners and/or have learned helplessness, the likelihood of them refusing to answer or to say "I don't know" is great. Types of questions that can help avoid such answers include, "Show me how you would……," and "Try to…" Sometimes, starting with one of two problems that students had success with can build momentum because they are more likely to respond both positively and with greater confidence. An alternative approach for establishing a dialogue with students is to ask them to represent what they did/define a concept in more concrete terms (Liedtke, 1988). Students can be provided concrete objects with which they illustrate their thoughts/actions. They also can be encouraged to illustrate their thinking by drawing pictures.

A third interview approach occurs when the student takes the role of teacher and demonstrates ("teaches") how to solve the problem to the teacher. As the student "teaches," the teacher notes errors and misconceptions. It is very important that the teacher not stop the student in the middle of teaching for correction purposes. To stop and re-teach at this point prevents the teacher from completely understanding the student's faulty mathematical thinking. Only after completely observing the student teach does the teacher get a complete "picture" of the student's faulty mathematical thinking.

Why is this approach helpful to students who have learning problems?

Flexible interviews help the teacher gain insight into a student's thinking. Because the various learning characteristics of students who have math learning problems can negatively impact learning, their mathematical thinking may be flawed. On the other hand, sometimes these students develop alternative approaches to math problem solving that are mathematically sound but which are "different" from what we typically teach. In either case, a teacher can learn a lot about a student's math problem solving abilities by implementing any of the techniques described above. When a teacher discovers faulty mathematical thinking, the teacher can then plan and implement appropriate instruction. The teacher may also gain insight into successful problem-solving strategies that the student uses. For example, a student may find it easier to use an alternative procedure for solving multi-digit multiplication, such as multiplying by place value:

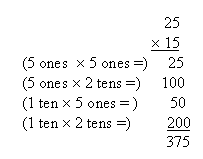
If a teacher was not familiar with this alternative procedure, then they may believe a student did not really understand how to multiply. However, when the student explains that he uses this procedure because he has difficulty remembering to use "zero" as a place value holder (when using the traditional procedure), or in lining up the numbers accurately, the teacher learns important instructional information. When other concepts or skills are taught, the teacher can help the student implement similar strategies that do not require extensive memory skills or the ability to write numbers in a linear spatial form. The more information about a student's learning that a teacher has, the more likely he/she will be able to implement instruction that accommodates that student's learning strengths and weaknesses.

[ back to Mathematics Dynamic Assessment ]