|
Bungee
m&m’s: Teacher Notes

MA.8.S.3.1
MA.912.A.3.11
Conceptual Understanding
Data Collection
Graphing
Line of Best Fit
Interpret Data
Procedural Knowledge
Organize Data
Graph Data
Make Predictions

Problem Solving
Reasoning
Connections
Representation

Several years ago amusement
parks introduced the thrill of bungee jumping to their guests. The
basic idea of bungee jumping was to jump from a great height with
an elastic cord tied to oneself so as to bounce up and down from the
end of the cord.
The need for advanced planning and testing of this apparatus is obvious.
Modeling the situation is a much safer means of determining safety
factors than making actual trials and perhaps fatal errors!

Students work in pairs

Each pair needs:
- 1 bungee cord (plastic
Slinky spring)
- 2 meter sticks
- 30 m&m’s
- 2 paperclips
- 1 paper cup

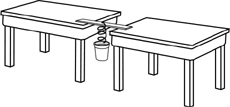
- Collect the Data
- Place the meter stick
level between two desks
- Using the paper clips, attach the cup to one end of the spring.
- Hook the other end of the spring to the meter stick so that
it hangs evenly between the two desks.
- Measure the distance from the bottom of the cup to the floor
with zero m&m’s in the cup.
- Record the distance in the table below.
- Add one m&m to the cup.
- After the cup comes
to a standstill, measure the distance to the floor again.
- Record the distance
in the table below.
- Repeat steps 6 through
8 four more times, adding one more m&m each time and
recording the data in the table below.
|
Weight
(# m&m's)
Independent Variable
X
|
Distance
to Floor (cm)
Dependent Variable
Y
|
|
0
|
|
|
1
|
|
|
2
|
|
|
3
|
|
|
4
|
|
|
5
|
|
- Graph the Data
- Graph your ordered
pairs on a coordinate plane with the Weight (# of m&m’s)
on the horizontal axis and the Distance (cm) on the vertical axis.
Be sure to label both axes and give your graph a title. When deciding
what units to put on your axes, keep in mind that you will need
to be able to use your graph to predict for shorter distances
and as many as 30 m&m’s.
- Analyze the Data
- Look at your graphed
points. What kind of correlation does this graph have? How can
you tell?
- As you add weight
to the Bungee Cup, what happens to the distance to the floor?
- By about how many
centimeters does the distance to the floor decrease every time
you increase the weight by one m&m?
- Draw the Line of Best
Fit
- Look at your graphed
points. Do they appear to lie along a straight line or a curve?
- Use a straight edge
to draw a "line of best fit" through the set of points
you have graphed. Be sure it passes through at least 2 of your
data points, leaving about the same number of other points on
each side of the "line of best fit." Be sure to extend
the line as far as possible!
- What was the distance
(cm) to the floor before any weight was added to the cup? How
can you tell this from your graph?
- How does that information
relate to the "line of best fit" on your graph?
- Describe in words
how to determine the distance from the floor (y) if you know the
weight (x).
- Make Predictions
- Use your graph with
the "line of best fit" and the data in your table to
predict how many m&m’s you will be able to put
into the cup so that the bungee cup comes as close to the floor
as possible without hitting the floor.
Total number of m&ms
Check your prediction . . . . .BE CAREFUL!!!

As a result of this activity,
students learn to model a real-life situation by collecting data from
a few trials, graphing the data, and then drawing a line of best fit
that can be used to make predictions

- Using the two points that
connected the "line of best fit," calculate the slope of
your line.
( , ) ( , )
slope: _______
m = _______
- Write the equation for
your "line of best fit" in slope-intercept form:
y = ______
|