|
Walking
the Plank: Student Worksheet
Name: ____________________________________

Ever thought you could
lose weight by the foot, not the pound?

Students work as a whole
class

- 1 bathroom scale
- 2 textbooks
- 1- 2’ X 8’ plank

- Collect the Data:
Mark the 2’ x 8’ plank into one foot increments
Place the plank on the bathroom scale and textbooks as shown below:
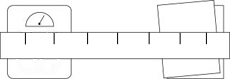
Weigh a volunteer person at each of the designated locations on the
plank.
|
Independent
Variable, X
Distance from Scale
(Feet)
|
Dependent Variable, Y
Weight
(Pounds)
|
|
0
|
|
|
1
|
|
|
2
|
|
|
3
|
|
|
4
|
|
|
5
|
|
|
6
|
|
- Graph the Data
Use "Distance from Scale (Feet)" as the horizontal scale
and "Weight (Pounds)" as the vertical scale. Plot ordered
pairs (X,Y).
- Read the Results
Looking at your graphed points, do they appear to lie along a straight
line or curve? Draw the line that best fits your data. Use the graph
to answer the following:
- Find the weight reading for the distances from the scale.
3.5 feet, _____ pounds
5.25 feet, _____ pounds
7 feet, _____ pounds
- How much does the weight reading decrease each time the person
moves another foot away from the scale?
____________________________________________________________________________________
How can you tell this from the graph?
____________________________________________________________________________________
- What is the person’s weight when standing directly on the
scale?
____________________________________________________________________________________
How can you tell this from the graph?
____________________________________________________________________________________
- Describe in words how to determine the weight reading if you know
how many feet the person is from the scale.
- Use your description to predict the weight reading for the person
when standing 4.75 feet from the scale. Show your work.
- Describe by equation how to determine the weight reading (Y) if
you know how many feet away (X) the person is from the scale:
Y= ____________________
- Use your equation to predict the weight reading for the person when
standing 6.5 feet away from the scale.

As a result of this activity,
students will learn how to collect, graph and interpret data.
|