|
A
Human Number Line: Teacher Notes

MA.5.A.6.4
MA.7.A.3.1
Conceptual Knowledge
Number Line
Symbols
Equality
Inequality
Procedural Knowledge
Addition
Subtraction
Solving Equations and Inequalities

Problem Solving
Reasoning
Communication
Connections
Representation

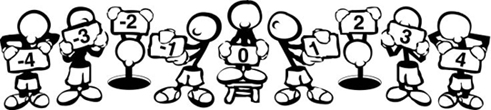
Can we make a human number
line?

Students work as a class

21 pieces of tagboard approximately
6" by 12" to represent the integers from -10 to 10. Each
piece of tagboard should have one integer written on it. Reverse side
is identical with open dot.


Pass out the integers and
line the students up to form a number line, zero in the middle, negative
numbers to the left, and positive numbers to the right.
- Strategy 1 Pictorial Representation:
Let P represent +1. Let N represent -1.
Reinforce the following concepts:
P and N are called a zero pair.
When adding, represent both numbers and combine zero pairs, if possible.
When subtracting, represent the first number and from that representation
subtract the second number.
Examples:
- 4 + (-3) = ?
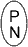 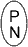
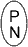 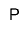
= +1
- -5 + (-2) = ?
N N N N N
N N
= -7
- 4 - (-3) = ?
P P P P
You need to subtract 3 N's, but there are no N's.
Add zero pairs (P N) until you can subtract 3 N's.
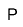 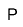 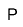 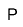
 

Now subtract 3 N's and the result is P P P P P P P = +7
- -4 - (-3) = ?
N N N N
You need to subtract 3 N's.
The result is N or -1.
- -3 -(-5) =?
N N N
You need to subtract 5 N's, but there are not enough N's.
Add zero pairs (P N) until you can subtract 5 N's.
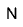 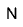  

Now subtract 5 N's and the result is P P = +2.
Once students have practiced
with pictorial representations, how would you make connections
to the abstract concepts and procedural skills of adding and subtracting
integers?
For example,
|
-3
- (-5)
|
= 0
+ 0 + (-3) - (-5) |
| |
= (1
+ -1) + (1 + -1) + (-3) - (-5) |
| |
= (1
+ 1) + (-1 + -1 + -3) - (-5) |
| |
= +2
+ (-5) - (-5) |
|
-3
- (-5)
|
= +2 |
- Strategy 2 Number Line:
Reinforce the following concepts related to the number line:
The first number in the expression is where you start on the number
line.
Operation symbols for adding (+) and subtracting (-) are called the
facing command. Addition means you face forward (right) and subtraction
means you face to the back (left).
Symbols inside the parenthesis (or with the second number) are called
the moving commands. The positive sign means to move forward, while
the negative sign means to move backwards.
Examples:
- 4 + (-3) = ?
Start at 4.
Face forward (to the right).
Move 3 spaces backwards.
End up at 1.
- -5 + (-2) = ?
Start at -5.
Face forward (to the right).
Move 2 spaces backwards.
End up at -7.
- 4 - (-3) = ?
Start at 4.
Face backward (to the left).
Move 3 spaces backwards.
End up at +7.
- -4 - (-3) = ?
Start at -4.
Face backwards (to the left).
Move 3 spaces backwards.
End up at -1.
- -3 - (-5) = ?
Start at -3.
Face backwards (to the left).
Move 5 spaces backwards.
End up at +2.

As a result of this activity,
students will have a better understanding of addition and subtraction
of integers and the relative size of numbers.

- Have students on the number
line show graphing for equations and inequalities.
- Have students at seats
write equation or inequality after seeing those graphed.
|