Adding and Subtracting Fractions with Mixed Numbers: Abstract Level

More Teaching Plans on this topic: Concrete, Representational

PHASE 1: Initial Acquisition of Skill

Teach Skill with Authentic Context

Description: continue to link adding fractions with mixed numbers without drawing to meaningful contexts such as the Pizza Party example described in the Representational/Drawing and Concrete Level Instructional Plans. This is especially important as you teach students to solve story problems without drawing using the FASTDRAW Strategy. Additionally, make explicit links to drawing experiences when teaching the abstract process.

Build Meaningful Student Connections

Purpose: to assist students to build meaningful connections between what they know about adding fractions with mixed numbers by drawing pictures and adding fractions with mixed numbers without drawing.

Learning Objective 1: Add fractions with mixed numbers using a “fraction place value mat” and a fraction number line.

Materials:

Teacher –

• A platform for writing/drawing so that all students can see (e.g. chalkboard/dry-erase board; chart paper; overhead projector.).
• The written objective: “add fractions with mixed numbers without drawing.” (*Highlight the words “without drawing” for cueing purposes.).
• Chalk/markers

Description:

1) L ink to students’ prior knowledge of adding fractions with mixed numbers by drawing to adding fractions with mixed numbers without drawing.

For Example:

You now know how to solve story problems and equations that involve addition of fractions with mixed numbers by drawing pictures that represent concrete materials. Let’s review how to add fractions with mixed numbers by drawing pictures. (Solve one problem with your students’ participation.)

2) I dentify the skill students will learn.

For Example:

Today I’m going to show you how to solve problems like this without drawing pictures. (Display the written objective: “add fractions with mixed numbers without drawing.”) What are we going to learn to do today? (Point to the written objective and elicit the response, “add fractions with mixed numbers without drawing.”) That’s right. We’re going to learn how to add fractions with mixed numbers by drawing. We’ll learn to add these kinds of problems by using numbers and symbols only. We’ll begin learning to do this with “fractions place value mats” and fraction number lines.

3) P rovide rationale/meaning for adding fractions with mixed numbers.

For Example:

You’ve learned how to add fractions with mixed numbers both by using concrete materials and by drawing. These are excellent strategies for solving problems like these. However, it takes quite a bit of time to do this and you may need to be able to do solve these problems more quickly. By the time we finish, you’ll be very good at solving these kinds of problems in your head using only the numbers and symbols.

[ back to top ]

Provide Explicit Teacher Modeling

Purpose: to provide students a clear teacher model of how to add fractions with mixed numbers without using concrete objects and without drawing pictures.

Learning Objective 1: Add fractions with mixed numbers using a fraction place value mat and a fraction number line.

Materials:

Teacher –

• Fraction place value mat: Has the same format as a place value mat representing “ONES” and “TENS” except the column to the right is labeled “Fractions” and the column to the left is labeled “Wholes.”

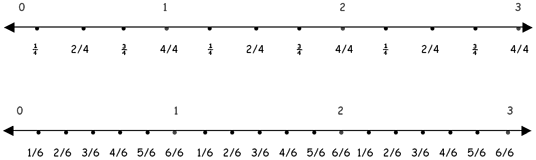
• “Long” fraction number lines that represent whole numbers and fractions with like denominators drawn on sentence strips:

Example of fraction number line (“fourths” and “sixths”):

*This example shows up to the whole number three. The actual fraction number line should extend to “10”

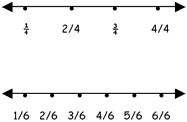
• “Shorter” fraction line strips that depict fractions with like denominators drawn on sentence strips (Each fraction strip should be made in the same proportion as the long fraction number line depicting whole numbers and fractions):

Example of fraction number line strips (“fourths” and “sixths”):

• A platform for visually displaying the fraction place value mats and fraction number lines so that all students can see.
• Pens/markers for writing.

Description:

A. Break down the skill of adding fractions with mixed numbers using a fraction place value mat and fraction number lines.

1) Discover the sign/operation.

2) Read the problem.

3) Write the “wholes” and fractions in appropriate columns of place value mat.

4) Introduce the fraction number line.

5) Add fractions using fraction number line.

6) Determine if one or more wholes can be made from adding the fractions by using the fraction number line.

7) “Regroup” the “whole(s)” made to the “whole” column of the fraction place value mat.

8) Add the wholes and write the number representing the sum.

9) Say the sum/total.

Learning Objective 2: Solve story problems and equations involving addition of fractions with mixed numbers using the FASTDRAW Strategy without drawing.

Materials:

Teacher –

• A visual display of the FASTDRAW and DRAW Strategy (for the “A” step in DRAW, omit “or draw and check.”)

F ind what you are solving for.
A sk yourself, “What is the important information?”
S et up the equation.
T ie down the sign.

D iscover the sign.
R ead the problem.
A nswer the problem.
W rite the answer

• A visual medium for writing (e.g. chalkboard, dry-erase board, chart paper.)
• Markers/pens for writing.
• Prepared story problems and/or equations that represent addition of fractions with mixed numbers. Color code whole numbers and fractions consistent with color-coding used to identify these concepts in story problems/equations used at the concrete level of understanding (e.g. 3 1/3 + 1 2/3 = __.)
• Fraction place value mats and fraction number lines (as needed).

A. Break down the skill of solving story problems and equations involving addition of fractions with mixed numbers using the FASTDRAW Strategy without drawing.

1) Introduce story problem.

2) Read the story problem aloud and then have students read it with you.

3) Teach finding the important information in the story problem and setting up an equation using the steps “FAST” from the “FASTDRAW” Strategy.

a. Find what you are solving for.
b. Ask yourself, what is the important information (circle it).
c. Set up the equation.
d. Tie down the sign.

4) Teach drawing solutions using the steps “DRAW” from the “FASTDRAW” strategy.

a. Determine the sign.
b. Read the problem.
c. Answer without drawing (using fraction place value mats and fraction number lines.)
d. Write the answer.

5) Model how to solve the story problem by relating the “answer” to the equation back to the story problem context.

6) Model how to draw solutions to equations by repeating the steps in#4 and #5 at least two or three more times with different division equations

[ back to top ]

.

Scaffold Instruction

Purpose: to provide students the opportunity to build their initial understanding of how to add fractions with mixed numbers without concrete materials or drawings, and to provide you the opportunity to evaluate your students’ level of understanding after you have initially modeled this skill.

Materials:

• Dependent on the skill you are Scaffolding Instruction for (See the materials listed for the specific skill you want to scaffold under Explicit Teacher Modeling)

Description:

*Scaffolding at the abstract level of instruction should occur using the same process as scaffolding instruction at the concrete and representational/drawing levels of instruction. (See the description of Scaffolding Instruction in the Concrete Level Instructional Plan for this math concept.) The steps listed for each skill during Explicit Teacher Modeling should be used as structure for scaffolding your instruction.

A. Scaffold instruction using a high level of teacher direction/support. Dependent on the needs of your students, you may want to continue to associate drawings to the abstract level process during this phase of scaffolding. Move to the next phase of scaffolding only when students demonstrate understanding and ability to respond accurately to your prompts.

B. Scaffold instruction using a medium level of teacher direction/support. If you associated drawings with the abstract process while scaffolding using a high level of teacher direction/support, then do not include drawings during this phase of scaffolding. Move to the next phase of scaffolding only when students demonstrate understanding and ability to respond accurately to your prompts.

C. Scaffold instruction using a low level of teacher direction/support. Students should actually add fractions with mixed numbers as you prompt them during this phase of Scaffolding Instruction. Move students to independent practice of the skill only after they demonstrate the ability to perform the skill with limited prompting from you.

[ back to top ]

Videos

There are no videos for the Abstract Level plan.

[ back to top ]