Rounding to Nearest 10 or 100: Concrete Level

More Teaching Plans on this topic: Representational, Abstract

PHASE 1: Initial Acquisition of Skill

Teach Skill with Authentic Context

Description:

Several story contexts including students helping the teacher decide the correct size box for storing books.

*The following description is an example of how you might implement this instructional strategy for rounding to the nearest ten using discrete counting objects. A similar process can be used for the other learning objectives in this plan.

Build Meaningful Student Connections

Purpose: to assist students to build meaningful connections between what they know about “counting on” and “counting back” by ones and rounding to the nearest ten.

Materials:

Teacher –

• A set of ten counting objects (e.g. counting chips, unifix cubes, beans.).
• “Round a set of objects to the nearest ten” written on a card or on the chalkboard/dry-erase board.

Description:

Learning Objective 1: Round to the nearest ten using discrete counting objects.

1) L ink to students’ prior knowledge of counting on and counting back.

For Example:

(Display a group of ten counting objects.) I have a group of ten counting chips. Count them aloud with me as I lay them in a row/line. (Count aloud with your students as you line the counting chips in a row.) We have ten counting chips here. You already know how to count on from one number to a number that is greater. Let’s do that now. Let’s count on from the fifth counting chip to the tenth counting chip. (Count to the fifth chip and then encourage your students to “count on” to ten with you. *Move each chip that you count on slightly above chips 1-5.) How many chips did we count on? (Elicit the response, “five.”) Good, we counted on five chips. Ok, now lets count back. Let’s start at the seventh chip and count back to the second chip. (Follow the same process as counting on.) How many chips did we count back? (Elicit the response, “five chips.”) Yes, we counted back five chips. We can use what we know about “counting on” and “counting back” to learn something new today.

2) I dentify the skill students will learn.

For Example:

Today we’re going to learn how to find which “ten” a set of objects is closest to. Another way to say this is that we are going to learn how to round a set of objects to the nearest ten. (Display a visual representation of the learning objective.)

3) P rovide rationale/meaning for rounding to the nearest ten.

For Example:

Being able to round a set of objects to the nearest ten, or being able to determine which ten a set of objects is closest to can be a very useful skill. For example, this skill can come in handy when you need to store things like CD’s, video games, baseball cards, or stamps. When you collect things such as these, you will need to keep them in a safe place like a box or notebook. Boxes and notebooks come in different sizes. Some may hold ten items, some twenty, some thirty or more. If you can determine which “ten” the number of CD’s or cards you have is closest to, then you can easily decide what size container you need. I’m going to show you what I mean now by showing you how to round to the nearest ten using some books I need to store away.

[ back to top ]

Provide Explicit Teacher Modeling

Purpose: to provide students a clear teacher model of rounding to the nearest “ten” or “hundred” with concrete materials.

Learning Objective 1: Round to the nearest ten using discrete counting objects.

Materials:

Teacher –

• A variety of discrete counting objects of sufficient number to represent various multiples of ten - up to ninety (e.g. books, unifix cubes, counting chips, beans, etc.)
• A visual platform from which to display concrete objects so all students can clearly see them (*there should be enough room to line concrete objects side-by-side in the form of a line in multiples of ten.).

Description:

Use “non-linked” discrete concrete objects to determine which multiple of ten a selected set of objects is closest to when the numerical value of the set lies between the two multiples of ten (e.g. Is a set of 17 objects closer in value/number to “10” or “20?”).

A. Break down the skill of using concrete objects to round to the nearest ten using discrete counting objects.

1) Introduce a story problem situation/context. - View Video

2) Read story aloud; then have students read with you

3) Line objects of the set in a row. - View Video

4) Count the total number of objects; say total.

5) Count on to higher ten with additional objects; say number “counted on.” - View Video

6) “Count back to lesser ten; say number “counted back.”

7) Compare “count on” group and “count back” group. - View Video

8) Determine closer ten.

9) Relate answer to story problem. - View Video

Learning Objective 2: Round to nearest hundred using “linked” proportional concrete materials.

Materials:

Teacher –

• A story problem depicting a situation where “rounding to the nearest hundred” is necessary to solve the story problem.
• Base-ten materials (ten sticks and one cubes)
• A visual platform from which to display concrete objects so all students can clearly see them (*there should be enough room to line ten sticks end-to-end to represent several hundreds (e,g, 0 to 300.).
• Language card with “nearest hundred” written.
• Markers/chalk for writing numerical values in word form.

A. Break down the skill of rounding to the nearest hundred using linked proportional (base-ten) concrete materials.

1) Introduce a story problem situation/context.

2) Read story aloud then have students read with you.

3) Represent number with base ten materials; line up in row.

4) Count and say the total.

5) Count on to the greater hundred by tens.

6) Say how many objects were “counted on.”

7) “Count back” to the lesser hundred.

8) Say how many objects were “counted back.”

9) Compare the “count on” group and the “count back” group.

10) Determine which group represents fewer objects.

11) Say which hundred the original group of objects is closer to and why.

12) Relate the solution to the story problem context.

Learning Objective 3: Round to the nearest ten using discrete concrete objects and a number line.

Materials:

Teacher –

• A variety of discrete counting objects of sufficient number to represent various multiples of ten - up to ninety (e.g. books, unifix cubes, counting chips, beans, etc.)
• A number line representing 1-90.
• A visual platform from which to display concrete objects so all students can clearly see them (*there should be enough room to line concrete objects side-by-side in the form of a line in multiples of ten.).
• A language card with the word “rounding” written.

A. Break down the skill of rounding to the nearest ten using discrete concrete objects and a number line.

1) Introduce the number line.

2) Represent value of numbers on number line with concrete objects. - View Video

3) Relate value of numbers on number line to concrete objects.

4) Represent number to be rounded with concrete objects.

5) Count on to “greater” ten with concrete objects; say total.

6) “Count back to “lesser” ten; say total. - View Video

7) Compare “count on” group and “count back” group; determine fewest objects.

8) Determine which “ten” the original group of objects is closer to.

9) Introduce the term “rounding.” - View Video

Learning Objective 4: Rounding to the nearest hundred using base-ten materials and a number line.

Materials:

Teacher –

• Number lines representing hundreds (e.g. “100” to “200;” “400” to “500;” “800 to “900”). Number lines should represent ten multiples. Color-coding the “tens” digit in the ten multiples to the color of the ten sticks can be a helpful cue for students with visual processing problems or attention difficulties. *The number lines should be measured so they are the same length as ten “ten sticks" laid side-to-side. Each ten multiple should be written so that it occurs at the beginning/end of the ten sticks.

For Example:

• Base-ten materials (ten sticks and one cubes).
• A visual platform from which to display concrete objects so all students can clearly see them (*there should be enough room to line concrete objects side-by-side in the form of a line in multiples of ten.).
• A language card with the word “rounding” written.

Description:

A. Break down the skill of rounding to the nearest ten using base-ten materials and a number line.

1) Introduce the number line.

2) Represent the value of numbers on the number line with base-ten materials (i.e. lay ten sticks side by side above number line).

For Example:

3) Relate value of numbers on number line to base-ten materials.

4) Represent number to be rounded with base-ten materials.

For Example:

5) “Count on” to the greater “hundred” and say total.

For Example:

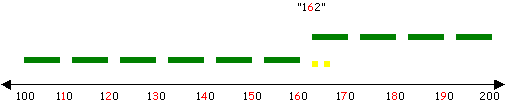
6) “Count back to the lesser “hundred” and say total.

For Example:

7) Compare “count on” group and the “count back” group; determine fewest objects.

8) Determine which “hundred” the original group of objects is closer to.

9) Review the term “rounding.”

Learning Objective 5: Round to the nearest ten and the nearest hundred with values that represent 100-999 using base-ten materials and a number line.

Materials:

Teacher –

number lines representing hundreds (e.g. “100” to “200;” “400” to “500;” “800 to “900”). Number lines should represent ten multiples. Color-coding the “tens” digit in the ten multiples to the color of the ten sticks can be a helpful cue for students with visual processing problems or attention difficulties. *The number lines should be measured so they are the same length as ten “ten sticks" laid side-to-side. Each ten multiple should be written so that it occurs at the beginning/end of the ten sticks.

For Example:

Base-ten materials (ten sticks and one cubes).
A visual platform from which to display concrete objects so all students can clearly see them (*there should be enough room to line concrete objects side-by-side in the form of a line in multiples of ten.).
A language card with the word “rounding” written.

Description:

A. Break down the skill of rounding to the nearest ten and the nearest hundred with values that represent 100-999 using base-ten materials and a number line.

1) Review the number line (Emphasize that it represents multiples of ten and cue students to the color-coding.)

2) Represent number to be rounded with base-ten materials.

For Example:

3) Identify whether you are rounding to the nearest ten or to the nearest hundred.

4) “Count on” to the greater “ten” or “hundred” using concrete materials and say the total.

Example for rounding to “tens:”

For Example for rounding to “hundreds:”

5) “Count back to the lesser “ten” or “hundred” and say total.

Example for rounding to “tens:”

Example for rounding to “hundreds:”

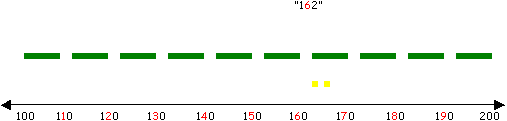
6) Compare the “count on” group and the “count back” group; determine fewest objects.

7) Determine which “ten” or “hundred” original group is closest to.

8 ) Review the term “rounding.”

[ back to top ]

Scaffold Instruction

*The following description is for the skill of “Rounding to the nearest hundred using base ten materials and a number line.”

Purpose: to provide students the opportunity to build their initial understanding of how to round to the nearest hundred using base-ten materials and a number line, and to provide you the opportunity to evaluate your students’ level of understanding after you have initially modeled this skill.

Materials:

Teacher –

• Number lines representing hundreds (e.g. “100” to “200;” “400” to “500;” “800 to “900”). Number lines should represent ten multiples. Color-coding the “tens” digit in the ten multiples to the color of the ten sticks can be a helpful cue for students with visual processing problems or attention difficulties. *The number lines should be measured so they are the same length as ten “ten sticks laid side-to-side. Each ten multiple should be written so that it occurs at the beginning/end of the ten sticks.

For Example:

• Base-ten materials (ten sticks and one cubes).
• A visual platform from which to display concrete objects so all students can clearly see them (*there should be enough room to line concrete objects side-by-side in the form of a line in multiples of ten.).
• A language card with the word “round to nearest hundred” written.
• Markers/chalk for writing

Students –

*For Low Level of Teacher Support

• Individual number lines representing hundreds (e.g. “100” to “200;” “400” to “500;” “800 to “900”). Number lines should represent ten multiples. Color-coding the “tens” digit in the ten multiples to the color of the ten sticks can be a helpful cue for students with visual processing problems or attention difficulties. *The number lines should be measured so they are the same length as ten “ten sticks laid side-to-side. Each ten multiple should be written so that it occurs at the beginning/end of the ten sticks.

For Example:

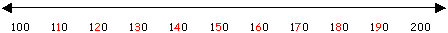
• Base-ten materials (ten sticks and one cubes)
• Pencils for writing

Description:

1) Scaffold Using a High Level of Teacher Direction/Support

a. Choose one or two places in the problem-solving sequence to invite student responses. Have these choices in mind before you begin scaffolding instruction. (Examples of choices are shown in red.) This example is for the number “324.”

Introduce the number line.

“What is this called (Point to the number line.)? (Elicit the response, “number line.”) Good. What does this number line represent? (Elicit the response, “numbers three-hundred through four-hundred.”) Yes. Do the numbers written on the number line increase by ones or by tens? (Elicit the response, “tens.”) Great!”

Count out a set of concrete objects that is between “three-hundred" and “four-hundred” and relate the total to the appropriate number on the number line by saying the total.

“ I have a set of base-ten materials that represent “three-hundred twenty four”. I’ll lay them on the number line and count aloud as I do this. Everyone count aloud with me. (Count aloud with your students (e.g. “three hundred ten, three-hundred twenty, three-hundred twenty-one, three-hundred twenty two…) What is the number we have represented? (Elicit the response, “three-hundred twenty-four.”) I’ll write “three-hundred twenty four” to help me remember what my materials represent. (Write “324” just above the last one cube and draw a line down to the number line to indicate where the number lies on the number line.”

Count on to the higher multiple of ten by adding additional objects in the line and then say the number of objects “counted on.”

“Now that I have represented my number, I have to count on to the higher hundred. Looking at my number line, I see that the higher hundred is four-hundred. (Point to “400” on the number line. When I’m rounding to the nearest hundred, I know it is easier to count on by tens rather than ones. I can start counting on from “three-hundred twenty” since it is easier to do this than counting by tens from “three-hundred twenty-four.” (“Count on” by placing ten sticks slightly above the original row of objects.) I counted on eight ten sticks to four hundred. (Point to the group of eight ten sticks.) I’ll write “eight tens” above the set of eight ten sticks. I also know that eight tens is eighty, so I’ll write “eighty” as well.” (Write both “eight tens” and “eighty” above the set of eight ten sticks.)

“Count back” to the lower multiple of ten and distinguish this subset of objects from the original set, then say aloud the number of objects counted back.

“Now that I’ve counted on to the higher hundred by tens, I need to count back to the lesser hundred by tens. Looking at my number line, I see that the lesser hundred is three-hundred. (Point to “300” on the number line. When I’m rounding to the nearest hundred, I know it’s easier to count back by tens rather than ones. I can start counting back from “three-hundred twenty” since it is easier to do this than counting by tens from “three-hundred twenty-four.” (“Count back” by moving ten sticks slightly above the original row of objects as you count back.) I counted back two ten sticks to three-hundred. (Point to the group of two ten sticks.) I’ll write “two tens” above the set of eight ten sticks. I also know that two tens is twenty, so I’ll write “twenty” as well.” (Write both “two tens” and “twenty” above the set of two ten sticks.)

Compare the total number of objects between the “count on” group and the “count back” group and determine which group has the fewest objects.

“Ok, now that I’ve counted on by tens to four hundred (Point to the set of eight “counted on” ten sticks) and counted back by tens to three hundred (Point to the set of two “counted back” ten sticks), I have to compare the two sets to see which one has fewer tens. Well, three-hundred twenty-four is about eight tens or eighty away from four hundred. (Point to the set of eight “counted on” ten sticks.) Three-hundred twenty-four is about two tens or twenty away from three-hundred (Point to the set of two “counted back” ten sticks.) Two tens or twenty is less than eight tens or eighty.” (Point to the words written above each set as you say this.)”

Determine which hundred the original group of objects is closer to and round to that hundred.

“In order to round to the nearest hundred (Show the language card that reads “round to the nearest hundred.”), I need to round to the hundred that is closest. Since “three-hundred twenty-four” is closer to “three-hundred” than it is to “four-hundred,” then I know I need to round to “three-hundred.” (Circle “300” on the number line.) I know “three-hundred twenty-four” is closer to “three-hundred” than it is to “four-hundred” because it is only about two tens or twenty away, while it is about eight tens or eighty away from “four-hundred.”” (Point to each set of “counted back” and “counted on” ten sticks as you say this.)

b. Maintain a high level of teacher direction/support for another example if students demonstrate misunderstanding/non-understanding; move to a medium level of teacher direction/support if students respond appropriately to the selected questions/prompts.

2) Scaffold Using a Medium Level of Teacher Direction/Support

a. Choose several more places in the problem-solving sequence to invite student responses. Have these choices in mind before you begin scaffolding instruction.

Introduce the number line.

“What is this called (Point to the number line.)? (Elicit the response, “number line.”) Good. What does this number line represent? (Elicit the response, “numbers three-hundred through four-hundred.”) Yes. Do the numbers written on the number line increase by ones or by tens? (Elicit the response, “tens.”) Great!”

Count out a set of concrete objects that is between “three-hundred" and “four-hundred” and relate the total to the appropriate number on the number line by saying the total.

“ I have a set of base-ten materials that represent “three-hundred thirty three”. How can I represent them on the number line? (Elicit the response, “lay them on the number line side-to-side.) Good. Everyone count aloud with me as I lay them out. (Count aloud with your students (e.g. “three hundred ten, three-hundred twenty, three-hundred thirty, three-hundred thirtty-one, three-hundred thirty two…). What number have we represented? (Elicit the response, “three-hundred thirty-three.”) What can I do to remember what value my base ten materials represent? (Elicit the response, “write three-hundred thirty-three just above the last one cube and draw a line down to the number line to indicate where the number lies on the number line.”) Great, I’ll do that now.

Count on to the higher multiple of ten by adding additional objects in the line and then say the number of objects “counted on.”

“Now that I have represented my number, I have to count on to the higher hundred. What’s the higher hundred? (Elicit the response, “four-hundred.”) Yes, four-hundred” is the higher hundred. (Point to “400” on the number line.) When we’re rounding to the nearest hundred, is it easier to count on by tens or by ones? (Elicit the response, “tens.”) Where do I start counting? (Elicit the response, “three-hundred thirtty.”) Great, I start counting on from “three hundred thirty” since it is easier to count on by tens from “three-hundred twenty” than from “three-hundred thirty-three. Where can I place the ten sticks as I count on? (Elicit the response, “above the other ten sticks.”) Count on with me as I lay the ten sticks down (“Count on” with your students by placing ten sticks slightly above the original row of objects.) How many tens did we count on? (Elicit the response, “seven.”) What does that equal? (Elicit the response, “seventy.”) How can I remember how many tens we counted on? (Elicit the response, write it above the set of seven ten sticks.) Good, I’ll do that now. (Write both “seven tens” and “seventy” above the set of seven ten sticks.)

“Count back” to the lesser ten and distinguish this subset of objects from the original set, then say aloud the number of tens counted back.

“Now that I’ve counted on to the higher hundred by tens, I need to count back to the lesser hundred by tens. What is the lesser hundred? (Elicit the response, “three-hundred.”) Yes, “three-hundred” is the lesser hundred. (Point to “300” on the number line.) When we’re rounding to the nearest hundred, is it easier to count on by tens or by ones? (Elicit the response, “tens.”) Where do I start counting back from? (Elicit the response, “three-hundred thirty.”) Great, I start counting back from “three hundred thirty” since it is easier to count back by tens from “three-hundred thirty” than from “three-hundred thirty- three." Where can I move the ten sticks as I count back? (Elicit the response, “above the other ten sticks.”) Count on with me as I move the each ten stick up. (“Count back” with your students by moving each ten stick you count on slightly above the original row of objects.) How many tens did we count back? (Elicit the response, “three.”) What does that equal? (Elicit the response, “thirty.”) How can I remember how many tens we counted back? (Elicit the response, write it above the set of two ten sticks.) Good, I’ll do that now. (Write both “three tens” and “thirty” above the set of three ten sticks.)

Compare the total number of objects between the “count on” group and the “count back” group and determine which group has the fewest objects.

“Ok, now that I’ve counted on by tens to four hundred (Point to the set of seven “counted on” ten sticks) and counted back by tens to three hundred (Point to the set of three “counted back” ten sticks), what do I do? (Elicit the response, “compare the two sets to see which one has fewer tens.) Good. Well, three-hundred thirty-three is about seven tens or seventy away from four hundred. (Point to the set of seven “counted on” ten sticks.) Three-hundred twenty-four is about three tens or thirty away from three-hundred (Point to the set of three “counted back” ten sticks.) Three tens or thirty is less than seven tens or seventy.” (Point to the words written above each set as you say this.)”

Determine which hundred the original group of objects is closer to and round to that hundred.

“In order to round to the nearest hundred (Show the language card that reads “round to the nearest hundred.”), I need to round to the hundred that is closest. Since “three-hundred thirty-three” is closer to “three-hundred” than it is to “four-hundred,” then I know I need to round to “three-hundred.” (Circle “300” on the number line.) I know “three-hundred thirty-threer” is closer to “three-hundred” than it is to “four-hundred” because it is only about three tens or thirty away, while it is about seven tens or seventy away from “four-hundred.”” (Point to each set of “counted back” and “counted on” ten sticks as you say this.) Why did I round to three-hundred thirty-three to “three-hundred” instead of “four-hundred?” (Elicit the response, “because “three-hundred thirty-three” is only about “thirty” away from three-hundred while it is about “seventy” away from “four-hundred.”)

b. Maintain a medium level of teacher direction/support for another example if students demonstrate misunderstanding/non-understanding; move to a low level of teacher direction/support if students respond appropriately to the selected questions/prompts.

3) Scaffold Using a Low Level of Teacher Direction/Support

a. When students demonstrate increased competence, do not model the process. Ask students questions and encourage them to provide all responses. Direct students to replicate the process at their desks as you work together.

Introduce the number line.

“What is the name for the what you have in front of you? Good. What does this number line represent? (Elicit the response, “numbers three-hundred through four-hundred.”) Yes. Do the numbers written on the number line increase by ones or by tens? (Elicit the response, “tens.”) Great!”

Count out a set of concrete objects that is between “three-hundred" and “four-hundred” and relate the total to the appropriate number on the number line by saying the total.

“ You all have a set of base-ten materials. How can you use them to represent the number “three-hundred sixty-seven” on the number line? (Elicit the response, “lay six ten sticks and seven one cubes on the number line side-to-side.) Where do you start? (Elicit the response, “at three-hundred.”) Good thinking, everybody do that now as I do it here. (Monitor students as they do this and check for understanding) Let’s count aloud the number we represented. (Count aloud with your students, “three hundred ten, three-hundred twenty, …). What number have we represented? (Elicit the response, “three-hundred sixty-seven.”) What can we do to remember what value my base ten materials represent? (Elicit the response, “write three-hundred sixty-seven just above the last one cube and draw a line down to the number line to indicate where the number lies on the number line.”) Great, let’s do that now. (Write this on your number line and then monitor students as they do it on their number lines.)

Count on to the higher multiple of ten by adding additional objects in the line and then say the number of objects “counted on.”

“Now that we’ve represented my “three-hundred sixty-seven” on our number lines, what do we do next? (Elicit the response, “count on to the higher hundred.”) Good. How can we do that with our materials? (Place one ten stick down as we count on to four-hundred.”) Good. Where to we start? (Elicit the response, “three-hundred seventy.”) Great. Where do we place the ten sticks as we count on to four-hundred? (Elicit the response, “above the ones we’ve already used to represent “three-hundred sixty-seven.”) Great thinking! Everybody, count on using your ten sticks. I’ll count on using my ten sticks. (Monitor students as they do this to check for understanding.) How many tens did you count on? (Elicit the response, “three.”) What does that equal? (Elicit the response, “thirty.”) What can you do to remember how many you counted on? (Elicit the response, write it above the set of eight ten sticks.) Good, let’s do that now. (Write both “three tens” and “thirty” above the set of three ten sticks and monitor students as they do this on their number lines.)

“Count back” to the lesser ten and distinguish this subset of objects from the original set, then say aloud the number of tens counted back.

“Now that we’ve counted on to “four-hundred,” what do we do next? (Elicit the response, “count on to the lower hundred.”) Good. How can we do that with our materials? (Move one ten stick up as we count back to three-hundred.”) Good. Where to we start? (Elicit the response, “three-hundred seventy.”) Great. Where do we move the ten sticks as we count backto three-hundred? (Elicit the response, “above the ones we’ve already used to represent “three-hundred sixty-seven.”) Great thinking! Everybody, count back using your ten sticks. I’ll count back using my ten sticks. (Monitor students as they do this to check for understanding.) How many tens did you count back? (Elicit the response, “seven.”) What does that equal? (Elicit the response, “seventy.”) What can you do to remember how many you counted on? (Elicit the response, write it above the set of seven ten sticks.) Good, let’s do that now. (Write both “seven tens” and “seventy” above the set of two ten sticks and monitor students as they do this on their number lines.)

Compare the total number of objects between the “count on” group and the “count back” group and determine which group has the fewest objects.

“Ok, now that we’ve counted on by tens to four hundred (Point to the set of three“counted on” ten sticks) and counted back by tens to three hundred (Point to the set of seven“counted back” ten sticks), what do we do? (Elicit the response, “compare the two sets to see which one has fewer tens.) Good. How will you compare the two sets? (Elicit the response, “see which set is less.”) Good. Which set is less? (Elicit the response, “the one with thirty.”) Good.

Determine which hundred the original group of objects is closer to and round to that hundred.

“In order to round to the nearest hundred what do we do? (Elicit the response, “circle the hundred that is closer to “three-hundred sixty-seven.”) Yes. Which hundred is closer? (Elicit the response, “four-hundred.”) How do you know this? (Elicit the response, “because “three-hundred sixty-seven” is only about “thirty” away from four-hundred while it is about “seventy” away from “three-hundred.”) Good. We round “three-hundred sixty-seven” to “four-hundred” by circling four-hundred. Everybody do this. (Monitor students as they do this to check for understanding.)

b. When you are confident students understand, ask individual students to direct the problem solving process or have the class direct you: Students ask questions and you and the students respond/perform the skill.

Learning Objective 2:

*Follow the same process as described above. Start with a high level of teacher direction/support, then fade your direction to a medium level of teacher direction/ support. Finally, when students demonstrate understanding, move to a low level of teacher direction/support until students can direct the performance of the skill. Use the learnable steps outlined under the teacher instruction strategy, “Explicit Teacher Modeling” for this skill to structure the steps you use during scaffolding.

[ back to top ]

Videos

Learning Objective 1: Round to the nearest ten using discrete counting objects.
View clip1

View clip2

View clip3

View clip4

View clip5

Learning Objective 3: Round to the nearest ten using discrete concrete objects and a number line.

View clip1

View clip2

View clip3

[ back to top ]